Least Common Multiple Of Exponents

Learning Outcomes

Observe the prime factorization of a number
Find the least mutual multiple of a listing of numbers

The word factor tin can be both a noun and a verb. To factor a number is to rewrite information technology by breaking it up into a production of smaller numbers. For example, we tin can cistron 24 by writing it every bit [latex]6\ast4[/latex]. We say that 6 and 4 are factors of 24. But so are 2 and 12. At that place are many ways to write this number.

A useful skill to have when doing algebra is the ability to rewrite numbers and expressions in helpful forms. For example, consider some different forms of the number 24.

[latex]24 \qquad \dfrac{72}{three} \qquad \sqrt{576} \qquad 6\ast4 \qquad 2\cdot2\cdot2\cdot3 [/latex].

Blended numbers, like 24, are natural numbers that can exist written as products of other natural numbers. Prime numbers are natural numbers that have only two possible factors, themselves and the number ane. The final course of 24 in the list higher up, [latex]2\cdot2\cdot2\cdot3 [/latex], is called itsprime number factorization. When we write the prime factorization of a number, we are writing information technology as a production of merely its prime factors. Being able to find the prime factorization of a blended number is an especially useful skill to have when doing algebra.

Prime Factorization

The prime number factorization of a number is the production of prime number numbers that equals the number.

Y'all may desire to refer to the following listing of prime numbers less than [latex]50[/latex] as y'all work through this section.

[latex]2,iii,v,seven,11,13,17,xix,23,29,31,37,41,43,47[/latex]

Tip: Knowing the first five prime numbers will come in handy when reducing fractions.

Prime Factorization Using the Factor Tree Method

One way to detect the prime factorization of a number is to make a factor tree. We beginning by writing the number, and and then writing it as the production of two factors. We write the factors below the number and connect them to the number with a small line segment—a "branch" of the factor tree.

If a cistron is prime number, we circumvolve information technology (like a bud on a tree), and exercise not factor that "co-operative" any further. If a factor is not prime, we echo this process, writing information technology as the product of ii factors and adding new branches to the tree.

We continue until all the branches finish with a prime. When the factor tree is complete, the circled primes give the states the prime factorization.

For case, permit's notice the prime number factorization of [latex]36[/latex]. We can start with any gene pair such as [latex]iii[/latex] and [latex]12[/latex]. Nosotros write [latex]3[/latex] and [latex]12[/latex] below [latex]36[/latex] with branches connecting them.

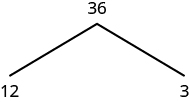
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end.
The cistron [latex]3[/latex] is prime, so we circle it. The factor [latex]12[/latex] is composite, and then we need to find its factors. Allow's apply [latex]3[/latex] and [latex]4[/latex]. We write these factors on the tree nether the [latex]12[/latex].

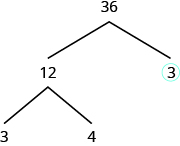
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end. Two more branches are splitting out from under 12. The right branch has the number 4 at the end and the left branch has the number 3 at the end.
The factor [latex]3[/latex] is prime, then nosotros circumvolve it. The factor [latex]iv[/latex] is composite, and it factors into [latex]2\cdot ii[/latex]. Nosotros write these factors under the [latex]4[/latex]. Since [latex]two[/latex] is prime, nosotros circle both [latex]2\text{s}[/latex].

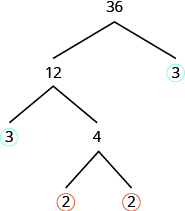
The prime factorization is the product of the circled primes. We mostly write the prime number factorization in society from least to greatest.

[latex]2\cdot 2\cdot 3\cdot 3[/latex]

In cases like this, where some of the prime factors are repeated, nosotros can write prime factorization in exponential course.

[latex]\brainstorm{array}{c}ii\cdot 2\cdot 3\cdot 3\\ \\ {ii}^{2}\cdot {iii}^{2}\end{array}[/latex]

Note that nosotros could have started our factor tree with whatsoever factor pair of [latex]36[/latex]. Nosotros chose [latex]12[/latex] and [latex]3[/latex], simply the issue would have been the same if we had started with [latex]2[/latex] and [latex]18, four[/latex] and [latex]ix,\text{ or }6\text{ and }half-dozen[/latex].

Detect the prime factorization of a blended number using the tree method

Find any factor pair of the given number, and employ these numbers to create ii branches.
If a factor is prime, that co-operative is complete. Circumvolve the prime.
If a gene is not prime number, write it as the product of a factor pair and continue the procedure.
Write the blended number as the production of all the circled primes.

example

Find the prime factorization of [latex]48[/latex] using the factor tree method.

Solution:

We tin start our tree using any factor pair of [latex]48[/latex]. Let's use [latex]2\text{ and }24[/latex]. We circumvolve the [latex]2[/latex] because it is prime number and and so that branch is complete.
Now we will factor [latex]24[/latex]. Let'southward utilize [latex]4\text{ and }6[/latex].
Neither factor is prime, then we do non circumvolve either.We factor the [latex]four[/latex], using [latex]two\text{ and }2[/latex].We factor [latex]6\text{, using }two\text{ and }3[/latex]. Nosotros circle the [latex]two\text{s and the }iii[/latex] since they are prime. Now all of the branches end in a prime number.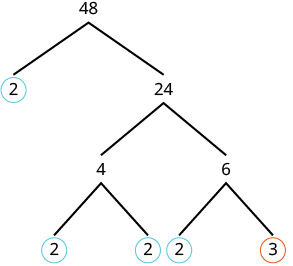
Write the product of the circled numbers.	[latex]ii\cdot 2\cdot 2\cdot 2\cdot 3[/latex]
Write in exponential form.	[latex]{2}^{iv}\cdot 3[/latex]

Bank check this on your own by multiplying all the factors together. The result should be [latex]48[/latex].

try information technology

The following video shows how to observe the prime factorization of [latex]lx[/latex] using the cistron tree method.

example

Discover the prime factorization of [latex]84[/latex] using the factor tree method.

try it

There are other methods that work well to detect the prime factorization of a number. Any method that factors out small primes repeatedly until at that place are just prime factors remaining is acceptable. See the video beneath for a demonstration of using stacked division to find a prime factorization.

Finding Least Common Multiples

Consider the multiples of two numbers, 3 and 4. What is the least common multiple between them?

Certainly three and 4 accept many multiples in common: 12, 24, 36, etc. But 12 is the smallest amidst them.

The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the LCM of [latex]3[/latex] and [latex]4[/latex] is [latex]12[/latex].

I of the reasons nosotros observe prime factorizations is to use them to find the to the lowest degree mutual multiple of two or more numbers. This will be useful when we add and subtract fractions with different denominators.

Prime Factors Method

Nosotros tin find the least common multiple of two numbers by inspecting their prime factors. We'll utilise this method to find the LCM of [latex]12[/latex] and [latex]18[/latex].

We outset by finding the prime factorization of each number.

[latex]12=2\cdot 2\cdot three \qquad[/latex] and [latex] \qquad 18=2\cdot 3\cdot 3[/latex]

And so we observe the largest case of each prime actualization in any one factorization. Here, nosotros encounter that the number 2 appears twice in the factorization of 12, merely merely one time in 18. And the number three appears twice in 18, merely only once in 12. So, nosotros select [latex]ii\cdot2[/latex] and [latex]3\cdot3[/latex] and multiply them together to notice the LCM.

[latex]12=2\cdot 2\cdot 3 \qquad \text{ and } \qquad 18=ii\cdot three\cdot 3[/latex]

[latex]\qquad two\cdot2 \qquad \qquad \ast \qquad \qquad iii\cdot3 [/latex].

[latex]\qquad\quad \qquad 2\cdot2\cdot3\cdot3=36[/latex].

The LCM of 12 and xviii is 36.

If a prime appears the same number of times in whatever factorization, only select i example. Let's find the LCM of a listing of numbers as an example.

Find the LCM of 12, 18, twenty, and 60. Offset we'll write the numbers as products of primes.

[latex]12 = 2\cdot2\cdot3 \qquad 18=ii\cdot3\cdot3 \qquad 20=2\cdot2\cdot5 \qquad sixty=2\cdot2\cdot3\cdot5[/latex]

Nosotros meet that the largest instance of the number ii appears in the numbers 12, 20, and threescore. Just we simply select one largest example. The largest instance of the number 3 appears in 18, where there are two factors of iii. And the number v appears once in 20 and once in lx, so nosotros'll select one 5.

The LCM of 12, 18, 20, and 60 is

[latex]2\cdot2\cdot3\cdot3\cdot5 = 180[/latex].

So, 180 is the smallest number that 12, eighteen, twenty, and 60 all divide evenly into.

Notice the LCM using the prime factors method

Notice the prime factorization of each number.
Inspect each factorization for the largest number of instances of each prime number actualization in each factorization
Select i prepare of each largest instance of each prime factor appearing.
Multiply the selected factors together to obtain the LCM.

It can exist helpful to write the prime factors next to each number, matching them vertically in columns, and then bringing downwards the primes in each column to collect the factors whose product is the LCM. The following examples illustrate this technique.

instance

Detect the LCM of [latex]fifteen[/latex] and [latex]xviii[/latex] using the prime factors method.

try it

case

Find the LCM of [latex]fifty[/latex] and [latex]100[/latex] using the prime factors method.

effort information technology

In the next video nosotros see how to find the Least Common Multiple by using prime number factorization.